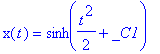
Oto rozwiązania symboliczne typowych równań różniczkowych. Komenda dsolve: równanie, ewentualnie z warunkami początkowymi + nazwa zmiennej zależnej. Uwaga - w równaniu należy pisać zawsze zmienną zależną z argumentem - zmienną niezależną.

>	dsolve(diff(x(t),t)=t*sqrt(1+x(t)^2),x(t));

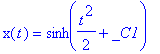
>	dsolve(diff(x(t),t$2)+x(t)=cos(t)+cos(2*t),x(t));

Poniżej rozwiązywanie równania w postaci szeregu potęgowego. Liczbę wyświetlanych wyrazów szeregu można modyfikować przyjmujac np. Order:=10. Wartość standardowa tego parametru 6.

>	dsolve({2*t^2*diff(x(t),t$2)+t^2*diff(x(t),t)+x(t)=1},x(t),series);

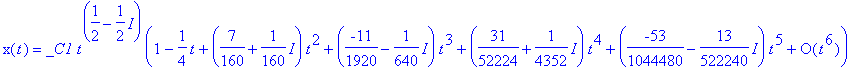
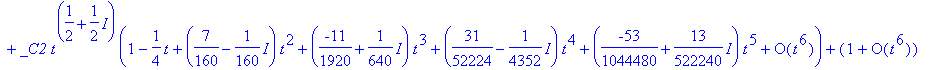
Zauważmy, że MAPLE czasami używa funkcji specjalnych, których nie znamy. O wyjaśnienie możemy zapytać ?WhittakerW;

>	dsolve(diff(x(t),t)=x(t)^2+t^2+1,x(t));

Nieco zmienione równanie i MAPLE nie znajduje rozwiązania dokladnego - brak jakiejkolwiek odpowiedzi. Co wtedy?

Możemy poszukiwać rozwiązań numerycznych. Wymaga to już zadania warunków początkowych tak, aby rozwiązaniem byla jednoznacznie określona funkcja.

Używamy opcji numeric w komendzie dsolve. Możemy także zmienić metodę numeryczną stosowaną przez MAPLE do obliczeń (por system pomocy ?dsolve/numeric). Proszę zauważyć, że wynikowi przypisalem nazwę tu - F -ale może to być dowolny ciąg znaków, aby w dalszym ciągu móc się do otrzymanej funkcji odwolywać.

>	dsolve(diff(x(t),t)=sqrt(x(t)^2+t^2+1),x(t));

>	F:=dsolve({diff(x(t),t)=sqrt(x(t)^2+t^2+1),x(0)=1},x(t),numeric);

>

F(0.5);

>

%[2];

>

rhs(%);

>	seq(F(i*0.01),i=0..10);

Możemy też narysować wykres otrzymanej funkcji. Używamy dodatkowego pakietu ,,plots" i  z niego komendy odeplot. Pierwszym argumentem jest nazwa funkcji, drugim - para zmienne, które mają być narysowane na wykresie, trzecim - zakres zmienności zmiennej niezależnej.

>	with(plots):

Warning, the name changecoords has been redefined

>	odeplot(F,[t,x(t)],t=-10..10);

>

Poniżej nieliniowe równanie Duffinga z wymuszaniem (prawa strona). Do narysowania wykresu rozwiązania z ustalonymi warunkami początkowymi stosujemy komendę DEplot z pakietu DEtools.Jej stosowanie zawiera wiele opcji - por. system pomocy. Zachęcam jednak do stosowania odeplot.

>	row:=diff(x(t),t$2)+0.25*diff(x(t),t)-x(t)+x(t)^3=0.4*cos(t);

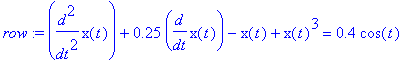
>	with(DEtools):

>	DEplot({row},x(t),t=-5..5,[[x(0)=0.1,D(x)(0)=-0.4]]);

>	G:=dsolve({row,x(0)=0.1,D(x)(0)=-0.4},x(t),numeric);

Zastosowanie większej liczby punktów pośrednich - opcja numpoints - wydluża obliczenia, ale poprawia dokladność, co widać w wygladzaniu wykresu.

>	odeplot(G,[t,x(t)],t=-5..50,numpoints=200); odeplot(G,[t,D(x)(t)],t=-5..50,numpoints=200); odeplot(G,[x(t),D(x)(t)],t=-5..50,numpoints=20000);

Poniżej dmonstrujemy wykresy rozwiązania równania wahadla z silą zewnętrzną. Uklad  jest silnie nieliniowy i rzędu 3 (rząd równania 2 + dodatkowy 1 na zmienną t, równanie jest nieautonomiczne. Dlatego zachowanie ukladu jest chaotyczne.

>	omega:=.3: A:=.9: r:=.5:

>	wah:=diff(x(t),t)=y(t),diff(y(t),t)=-omega*y(t)-sin(x(t))+A*cos(r*t);

>	f:=dsolve({wah, x(0)=1.2,y(0)=.2},{x(t),y(t)},numeric,output=listprocedure);

>	with(plots): odeplot(f,[x(t),y(t)],0..200,numpoints=200);

>	odeplot(f,[t,x(t)],0..200);

>	odeplot(f,[t,y(t)],0..200);

Poniżej równanie Lorenza - pierwsze równanie, w którym zaobserwowano chaos

>	lorenz:=diff(x(t),t)=sigma*(y(t)-x(t)), diff(y(t),t)=r*x(t)-y(t)-x(t)*z(t), diff(z(t),t)=x(t)*y(t)-b*z(t);

>	sigma:=10:

>

b:=8/3:

>

r:=28:

>	ff:=dsolve({lorenz,x(0)=.2,y(0)=.1,z(0)=.5 },{x(t),y(t),z(t)},type=numeric,output=listprocedure);

>	fx:=subs(ff,x(t));

>	fy:=subs(ff,y(t)): fz:=subs(ff,z(t)):

>

fx(0);

>

fx(0.3);

>	with(plots): odeplot(ff,[t,x(t)],0..100);

Warning, the name changecoords has been redefined

Warning, cannot compute solution further right of 86.8255095722534236

>	odeplot(ff,[t,y(t)],0..60);

>	odeplot(ff,[t,x(t)],0..60);

>	odeplot(ff,[t,z(t)],0..60);

>	odeplot(ff,[x(t),y(t)],15..60);

>	odeplot(ff,[x(t),y(t),z(t)],10..50);

>	odeplot(chaos,[x(t),y(t)],0..60);

>	odeplot(chaos,[x(t),y(t),z(t)],0..60);

Równanie Chua opisuje chaos w prostym nieliniowym obwodzie elektrycznym.

>

restart;

>	g:=x->c*x+((d-c)/2)*(abs(x+1)-abs(x-1)):

>	a:=15: b:=25.58: c:=-5/7: d:=-8/7:

>	chua:=diff(x(t),t)=a*(y(t)-x(t)-g(x(t))),       diff(y(t),t)=x(t)-y(t)+z(t),       diff(z(t),t)=-b*y(t):

>	warpocz:=x(0)=.2,y(0)=.3,z(0)=.1:

>	with(DEtools):

>	with(plots):

Warning, the name changecoords has been redefined

>	F:=dsolve({chua,warpocz},numeric,output=listprocedure);

>	odeplot(F,[x(t),y(t)],0..150);

>	odeplot(F,[x(t),z(t)],0..150);

>	odeplot(F,[z(t),y(t)],0..150);

>	odeplot(F,[x(t),y(t),z(t)],0..150);

Rozwiązania numeryczne mogą być mylące. W poniższym równaniu mianownik może bardzo zbliżać się do 0. Wtedy dokladnośc jest praktycznie iluzoryczna. Widzimy, że gdy powiększamy kawalek wykresu, to obrazek powiększony może być nawet jakościowo inny niż odpowiedni fragment na pierwszym plocie. Porównajmy kolory kolejnych krzywych.

>	row:=diff(x(t),t,t)=1/(sin(x(t)));

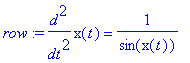
>	with(DEtools):

>	DEplot(row,x(t),t=-5..5,[[x(0)=1,D(x)(0)=0],[x(0)=2,D(x)(0)=0],[x(0)=3,D(x)(0)=0],[x(0)=4,D(x)(0)=0]],linecolour=[red,yellow,green,blue],stepsize=.01);

>	DEplot(row,x(t),t=1.5..2.5,[[x(0)=1,D(x)(0)=0],[x(0)=2,D(x)(0)=0],[x(0)=3,D(x)(0)=0],[x(0)=4,D(x)(0)=0]],linecolour=[red,yellow,green,blue],stepsize=.001);

>